Performance Benchmarks
How does second_quantization compare to established quantum simulation libraries? In this benchmark, we evaluate the performance of our package against two popular alternatives:
We focus on the time required to construct the Hamiltonian matrix for a chain of spinful fermions. Since second_quantization is designed for symbolic-to-matrix conversion, we don't benchmark diagonalization times (which are identical across packages once the matrix is built).
Setup
Import Libraries
First, we import the necessary tools from each package:
import time
from timeit import timeit
import numpy as np
import sympy
from sympy.physics.quantum.fermion import FermionOp
from sympy.physics.quantum.boson import BosonOp
from sympy.physics.quantum import Dagger
import matplotlib.pyplot as plt
from second_quantization import hilbert_space
from quspin.basis import (
boson_basis_1d,
spinful_fermion_basis_1d,
spinless_fermion_basis_1d,
tensor_basis,
)
from quspin.operators import hamiltonian
import openfermion
from openfermion.transforms import get_sparse_operator
from openfermion.ops import FermionOperator
Define the Test System
We construct a spinful fermion chain with:
- Nearest-neighbor hopping (kinetic energy for spin-up and spin-down)
- Onsite Coulomb interaction (repulsion between opposite spins on the same site)
- Chemical potential (controls the average particle number)
Here's the implementation for second_quantization:
def build_spinful_chain_hamiltonian(n):
"""
Builds a chain Hamiltonian for spinful fermions with:
- nearest-neighbor hopping for both spins,
- onsite Coulomb interaction between up/down spins,
- chemical potential for both spins.
There are 2*n fermionic modes: c_{i,up}, c_{i,down} for i in 0..n-1.
"""
t, U, mu = sympy.symbols('t U mu', real=True)
ops_up = [FermionOp(fr"c_{{{i},\uparrow}}") for i in range(n)]
ops_dn = [FermionOp(fr"c_{{{i},\downarrow}}") for i in range(n)]
hopping = 0
interaction = 0
chemical = 0
for i in range(n - 1):
# Hopping for up
hopping += -t * (Dagger(ops_up[i]) * ops_up[i + 1] + Dagger(ops_up[i + 1]) * ops_up[i])
# Hopping for down
hopping += -t * (Dagger(ops_dn[i]) * ops_dn[i + 1] + Dagger(ops_dn[i + 1]) * ops_dn[i])
for i in range(n):
# Onsite Coulomb interaction
interaction += U * (Dagger(ops_up[i]) * ops_up[i]) * (Dagger(ops_dn[i]) * ops_dn[i])
# Chemical potential for both spins
chemical += -mu * (Dagger(ops_up[i]) * ops_up[i] + Dagger(ops_dn[i]) * ops_dn[i])
H = hopping + interaction + chemical
ops = ops_up + ops_dn
return H, ops
Let's visualize the Hamiltonian for a small two-site system:
H, ops = build_spinful_chain_hamiltonian(2)
sympy.Eq(sympy.Symbol('H'), H.factor())
$\displaystyle H = U {{c_{0,\uparrow}}^\dagger} {c_{0,\uparrow}} {{c_{0,\downarrow}}^\dagger} {c_{0,\downarrow}} + U {{c_{1,\uparrow}}^\dagger} {c_{1,\uparrow}} {{c_{1,\downarrow}}^\dagger} {c_{1,\downarrow}} - \mu \left({{c_{0,\downarrow}}^\dagger} {c_{0,\downarrow}} + {{c_{0,\uparrow}}^\dagger} {c_{0,\uparrow}}\right) - \mu \left({{c_{1,\downarrow}}^\dagger} {c_{1,\downarrow}} + {{c_{1,\uparrow}}^\dagger} {c_{1,\uparrow}}\right) - t \left({{c_{0,\downarrow}}^\dagger} {c_{1,\downarrow}} + {{c_{1,\downarrow}}^\dagger} {c_{0,\downarrow}}\right) - t \left({{c_{0,\uparrow}}^\dagger} {c_{1,\uparrow}} + {{c_{1,\uparrow}}^\dagger} {c_{0,\uparrow}}\right)$
Implementations for Other Libraries
For a fair comparison, we implement the same Hamiltonian in OpenFermion and QuSpin:
def build_spinful_chain_hamiltonian_openfermion(n, t=1.0, U=1.0, mu=0.0):
"""
Builds a chain Hamiltonian for spinful fermions using OpenFermion.
- n: number of sites
- t: hopping amplitude
- U: onsite interaction
- mu: chemical potential
Returns: FermionOperator
"""
H = FermionOperator()
for i in range(n - 1):
# Hopping for up
H += -t * (FermionOperator(f'{2*i}^ {2*(i+1)}') + FermionOperator(f'{2*(i+1)}^ {2*i}'))
# Hopping for down
H += -t * (FermionOperator(f'{2*i+1}^ {2*(i+1)+1}') + FermionOperator(f'{2*(i+1)+1}^ {2*i+1}'))
for i in range(n):
# Onsite Coulomb interaction
H += U * FermionOperator(f'{2*i}^ {2*i} {2*i+1}^ {2*i+1}')
# Chemical potential for both spins
H += -mu * (FermionOperator(f'{2*i}^ {2*i}') + FermionOperator(f'{2*i+1}^ {2*i+1}'))
return H
def quspin_sparse_hamiltonian(L):
"""
Builds a sparse Hamiltonian for a 1D spinful fermion model.
"""
J = 1.0 # Hopping matrix element
U = 2.0 # Onsite interaction strength
mu = 0.5 # Chemical potential
start = time.time()
basis = spinful_fermion_basis_1d(L=L)
time_basis = time.time() - start
# Only define one direction for hopping; QuSpin adds the Hermitian conjugate
hop_right = [[-J, i, (i + 1) % L] for i in range(L)] # hopping to the right PBC
hop_left = [[J, i, (i + 1) % L] for i in range(L)] # hopping to the left PBC
potential = [[-mu, i] for i in range(L)]
interaction = [[U, i, i] for i in range(L)]
static = [
["+-|", hop_left], # up hop left
["-+|", hop_right], # up hop right
["|+-", hop_left], # down hop left
["|-+", hop_right], # down hop right
["n|", potential], # Onsite potential for spin up
["|n", potential], # Onsite potential for spin down
["n|n", interaction], # Spin up-spin down interaction
]
return static, basis, time_basis
Benchmark Methodology
We measure two key performance metrics:
Setup Time
The time required to prepare the computational infrastructure—building operator bases and symbolic representations—before matrix construction.
Matrix Construction Time
The time to build the actual sparse matrix representation of the Hamiltonian.
max_n = 10
ns = list(range(2, max_n + 1))
for i, n in enumerate(ns):
# Second quantization
H, ops = build_spinful_chain_hamiltonian(n)
start_basis_sq = time.time()
operator_dict = hilbert_space.basis_operators(ops, sparse=True)
basis_times_sq.append(time.time() - start_basis_sq)
start_1 = time.time()
hilbert_space.to_matrix(H, operators=ops, sparse=True, operator_dict=operator_dict)
sparse_times_sq.append(time.time() - start_1)
# QuSpin
static, basis, time_basis_qspin = quspin_sparse_hamiltonian(n)
basis_times_quspin.append(time_basis_qspin)
start_2 = time.time()
H_quspin = hamiltonian(static, [], basis=basis, dtype=np.float64)
H_sparse = H_quspin.as_sparse_format().static
sparse_times_quspin.append(time.time() - start_2)
# OpenFermion
start_of = time.time()
H = build_spinful_chain_hamiltonian_openfermion(n)
basis_times_of.append(time.time() - start_of)
sparse_time_of = time.time()
H_sparse_openfermion = get_sparse_operator(H)
sparse_times_of.append(time.time() - sparse_time_of)
Results
The following plots compare the three libraries across system sizes (number of fermionic modes):
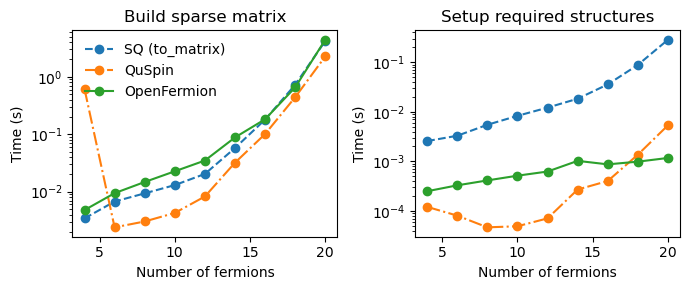
Reusability Advantage
A unique strength of second_quantization is the ability to reuse Hamiltonian matrix representation across multiple parameter choices. Once you've built the symbolic structure, generating matrices with different parameter values is extremely fast:
H, ops = build_spinful_chain_hamiltonian(n)
H_dict = hilbert_space.to_matrix(H, operators=ops, sparse=True)
f_H = hilbert_space.make_dict_callable(H_dict)
# total time for 50 runs
t = timeit(stmt='f_H(U=1, t=1, mu=.1)', number=50, globals=globals())
print("Time per-call (s):", t / 50)
Time per-call (s): 0.08301087105646729
This makes second_quantization particularly well-suited for:
- Parameter sweeps and phase diagram calculations
- Variational algorithms requiring many Hamiltonian evaluations
- Machine learning pipelines with parameterized quantum systems
Summary
second_quantization delivers competitive performance while offering a flexible, symbolic workflow. The ability to separate symbolic construction from numerical evaluation makes it an excellent choice for research workflows that require exploring multiple parameter regimes.
Mixed Fermion-Boson Construction
To compare mixed particle systems, we consider a chain of coupled quantum dots.
Each dot is a fermionic mode c_i that is coupled to its own bosonic resonator
mode a_i. The Hamiltonian is
$$ H = -t \sum_i \left(c_i^\dagger c_{i+1} + c_{i+1}^\dagger c_i\right) + \sum_i \left[\epsilon c_i^\dagger c_i + \omega_r a_i^\dagger a_i + g\left(c_i^\dagger a_i + c_i a_i^\dagger\right)\right]. $$
The first term couples neighboring dots. The remaining terms are one
Jaynes-Cummings Hamiltonian per dot-resonator pair. We truncate each resonator
to photon_cutoff + 1 states, so the total Hilbert-space dimension is
(2 * (photon_cutoff + 1)) ** n for n dots.
Define the Test System
For second_quantization, this is quite straight forward:
def build_dot_resonator_chain_hamiltonian(n):
"""Build a chain of dots, each coupled to one resonator."""
hopping, dot_energy, resonator_energy, coupling = sympy.symbols(
"t epsilon omega_r g", real=True
)
dots = [FermionOp(f"c_{i}") for i in range(n)]
resonators = [BosonOp(f"a_{i}") for i in range(n)]
symbolic_hamiltonian = sum(
dot_energy * Dagger(dot) * dot
+ resonator_energy * Dagger(resonator) * resonator
+ coupling * (Dagger(dot) * resonator + dot * Dagger(resonator))
for dot, resonator in zip(dots, resonators)
)
symbolic_hamiltonian += -hopping * sum(
Dagger(left) * right + Dagger(right) * left
for left, right in zip(dots, dots[1:])
)
return symbolic_hamiltonian, dots + resonators
QuSpin Implementation
QuSpin uses a tensor basis with the fermionic dot basis first and the bosonic
resonator basis second. Its operator strings use | to separate the two
subspaces: "+-|" is a fermionic hopping term and "+|-" is the
dot-resonator coupling term $c_i^\dagger a_i$.
def quspin_dot_resonator_chain(n, photon_cutoff):
hopping = 1.0
dot_energy = 0.5
resonator_energy = 1.0
coupling = 0.2
dot_basis = spinless_fermion_basis_1d(L=n)
resonator_basis = boson_basis_1d(L=n, sps=photon_cutoff + 1)
basis = tensor_basis(dot_basis, resonator_basis)
hop_left = [[hopping, i, i + 1] for i in range(n - 1)]
hop_right = [[-hopping, i, i + 1] for i in range(n - 1)]
dot_onsite = [[dot_energy, i] for i in range(n)]
resonator_onsite = [[resonator_energy, i] for i in range(n)]
dot_resonator = [[coupling, i, i] for i in range(n)]
static = [
["+-|", hop_left],
["-+|", hop_right],
["n|", dot_onsite],
["|n", resonator_onsite],
["+|-", dot_resonator],
["-|+", dot_resonator],
]
return static, basis
Results
Scaling with System Size
def mixed_matrix_times(n, photon_cutoff):
"""Time sparse-matrix construction after each package builds its basis."""
symbolic_hamiltonian, operators = build_dot_resonator_chain_hamiltonian(n)
operator_dict = hilbert_space.basis_operators(
operators,
sparse=True,
truncation=photon_cutoff,
)
start = time.time()
hilbert_space.to_matrix(
symbolic_hamiltonian,
operators=operators,
sparse=True,
operator_dict=operator_dict,
truncation=photon_cutoff,
)
time_sq = time.time() - start
static, basis = quspin_dot_resonator_chain(n, photon_cutoff)
start = time.time()
quspin_hamiltonian = hamiltonian(static, [], basis=basis, dtype=np.float64)
quspin_hamiltonian.as_sparse_format().static
time_quspin = time.time() - start
return time_sq, time_quspin
size_cutoff = 2
mixed_sizes = list(range(1, 6))
mixed_times_sq = []
mixed_times_quspin = []
for n in mixed_sizes:
time_sq, time_quspin = mixed_matrix_times(n, size_cutoff)
mixed_times_sq.append(time_sq)
mixed_times_quspin.append(time_quspin)
Scaling with Resonator Truncation
We now fix the chain to three dot-resonator pairs and vary the maximum photon number retained for each resonator.
fixed_size = 3
truncations = list(range(1, 6))
truncation_times_sq = []
truncation_times_quspin = []
for photon_cutoff in truncations:
time_sq, time_quspin = mixed_matrix_times(fixed_size, photon_cutoff)
truncation_times_sq.append(time_sq)
truncation_times_quspin.append(time_quspin)
